Preview of Hyperproof
A Sample Proof
In Hyperproof, a proof begins with some initial information, generally provided in the form of a diagram depicting a blocks world (which we call a "situation") plus one or more sentences (expressed in the language of first-order logic). This initial information is called the given information, and the aim of a proof is to demonstrate that one or more characteristics hold of the given information. For example, we may want to show that a particular sentence follows logically from the given information, or that we cannot determine the size or shape of a particular block on the basis of the given information.
Below, we show a sample proof. This proof demonstrates that the sentence SameShape(c,d) ("c is the same shape as d") is a consequence of the given information. Here, the given information consists of the situation displayed plus two sentences.
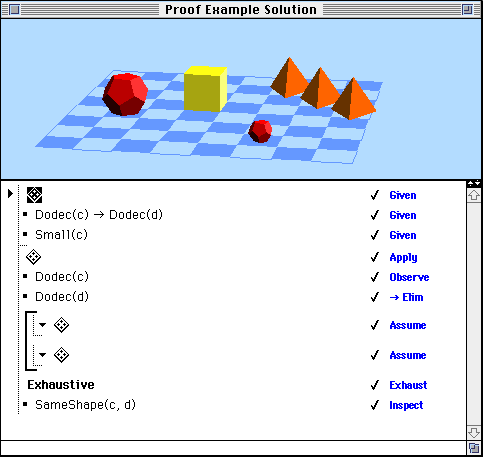
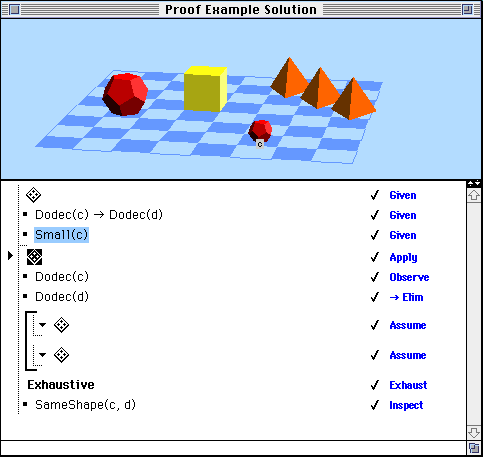
Notice that this proof has several steps containing a diamond icon: [missing icon]. These are steps in which the user has made modifications to the situation in the course of the proof. For example, in the user's first step, shown in the following image, the label " c" has been applied to the small dodecahedron, based on the information provided by the second given sentence.
We won't try to explain the various rules used in this proof. Suffice it to say that the proof goes on to show that the block named "d" must be one or the other of the two dodecahedra, and hence that, whichever it is, c and d have the same shape.
Hyperproof Diagrams
The diagrams in Hyperproof can give you more or less information about the blocks world depicted, thanks to certain conventions we use to show partial information. For example, here is a situation in which a considerable amount of information is left unspecified:

In this diagram, the barrel-shaped icons indicate the positions of blocks of unknown size. The barrel marked with an orange triangle represents a tetrahedron of unknown size. The barrel marked with a question mark indicates a block of unknown size and shape. Notice that there is also a paper-bag-shaped icon toward the center of the grid. This represents a block whose size we know but whose shape we do not know. Finally, the tetrahedron sitting off to the right of the grid represents a block whose location is currently unknown.
Reasoning goals
The sample proof we saw before had a relatively traditional goal: to show that a particular sentence is a consequence of the given information. Its goal is specified in a goal window associated with the proof:

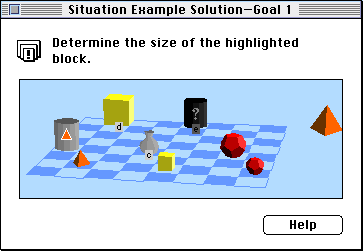
In Hyperproof, there are a multitude of different types of possible reasoning goals. For example a proof that begins with the above diagram (plus some sentences) might ask the user to determine the size of the block named "e":
Or it might ask the user to show that you cannot determine the shape of the block named "c":

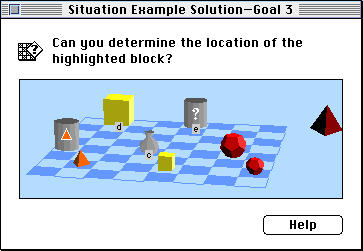
Or it might ask the user whether the location of the large tetrahedron can be determined on the basis of the diagram and the given sentences.
There are a total of 27 different types of goals that might appear in a Hyperproof problem. In addition to various "diagrammatic" goals like those above, students might be asked to prove that a specified sentence is or is not a consequence of the given information, or that the given information is or is not consistent.
This flexibility allows students to learn the techniques of valid reasoning in a setting that parallels ordinary, everyday analytical reasoning. When students learn logic using a standard deductive system, the main skill they learn is that of constructing proofs of antecedently specified sentences. But this is rarely, if ever, the kind of reasoning they are called on to perform in everyday life.
More commonly, they are faced with a reasoning task in which they have a generically specified goal and must determine whether the goal can be satisfied with the information at hand. Think of Sherlock Holmes trying to identify a murderer: He is not told in advance that the butler did it, and asked to prove this assertion. Rather his goal is to figure out who did it, if that is possible from the given information, and if not, to recognize that more evidence must be gathered.
Hyperproof allows us to teach skills appropriate to this more natural form of analytical reasoning. But it does so without giving up the rigor offered by a traditional deductive system.
Hyperproof's Proof System
The proof system in Hyperproof is an extension of the Fitch-style deductive system presented in The Language of First-order Logic. Because of this, Hyperproof can be used as a simple proof checker for instructors using this text to teach a standard introductory course in logic. This has the value of giving students instant feedback about whether they are applying inference rules correctly.
The full proof system, however, is both more powerful and more natural than ordinary syntactic systems. Here, for example, is a simple Hyperproof problem, one in which students are asked, first, whether they can identify which block is named "a", and second, whether it follows from the given information that there are two or more large tetrahedra. The given sentences tell us that block b is a dodecahedron, that b is to the left of block a (from our perspective), and that block a is large. (Note that we already know that one of the tetrahedra, the one farthest back, is large.)

If you solved this problem in your head, you probably went through the following reasoning: First, since b is a dodecahedron, it must be one or the other of the two dodecahedra in the sixth column. In either case block a, which must be farther right than b, has to be the tetrahedron of undetermined size. Since we know that a is large, we can conclude that there are two large tetrahedra.
The Hyperproof solution to this problem corresponds exactly to this intuitive reasoning. In contrast, if this problem were to be translated completely into the first-order language, the corresponding proof would be several hundred steps long! If you would like to see a step-by-step illustration of the Hyperproof solution, click here.
A Sample Solution
The student begins by breaking into two cases, corresponding to the possible assignments of the names "a" and " b". Block b might be the front dodecahedron and block a the tetrahedron on the right:
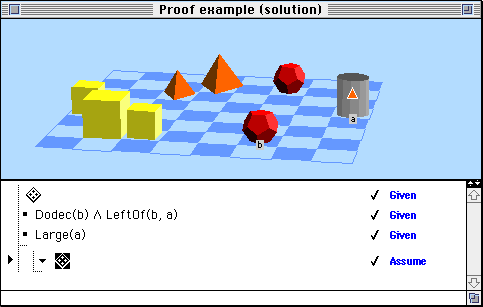
Or block b might be the back dodecahedron:
[missing image]
Next the student claims, correctly, that these two cases are exhaustive, given the information in the first sentence:
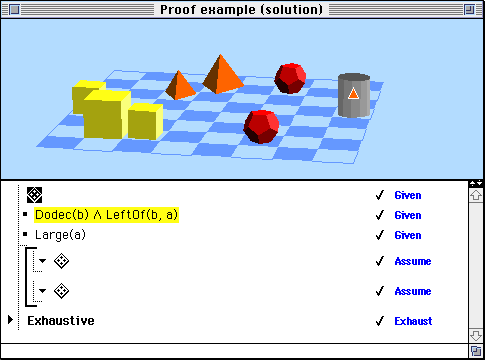
From this the student can conclude that block a is definitely the tetrahedron on the right, solving the first goal:
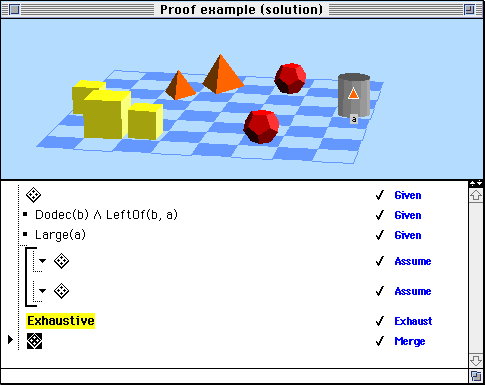
And hence, since we are told that a is large, we can apply this information to the diagram:
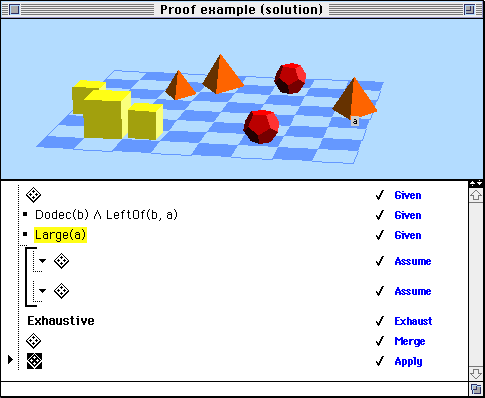
This allows the student to observe that there are at least two large tetrahedra, solving the second goal:
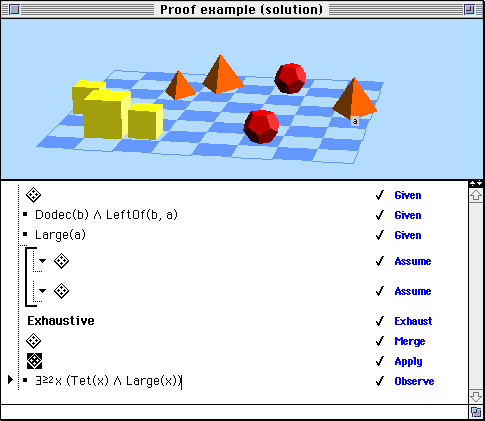
This concludes the student's solution.